Arbeitsauftrag: Konfirmatorische Faktorenanalyse

Veröffentlichungsdatum

16. Januar 2025

Tutorialreihe zum UK Fragebogenentwicklung

1 Einführung

In diesem Tutorial werden Sie darauf vorbereitet, wie Sie die Daten aus Ihrem im UK erstellten Fragebogen mithilfe einer Konfirmatorischen Faktorenanalyse (CFA) in R auswerten können. Dazu arbeiten wir zunächst mit einem Beispieldatensatz, an dem wir die grundlegenden Schritte der Auswertung nachvollziehen.

Ein Schwerpunkt wird sein, wie wir Modelltests in R durchführen. Insbesondere schauen wir uns im Detail an, wie man den Modelltest für das eindimensionale $\tau$-kongenerische Modell in R durchführt und dabei die Modellparameter schätzt und interpretiert. Zusätzlich zum Modelltest werden wir uns weitere Methoden anschauen, wie man den Modellfit beurteilen kann.

Wir werden diese Methoden zunächst einmal gemeinsam durcharbeiten, bevor Sie den vollständigen Ablauf dann eigenständig im Arbeitsauftrag anwenden.

1.1 Auffrischung der R Grundlagen

Da das Arbeiten mit R bei einigen von Ihnen vielleicht schon eine Weile zurückliegt, lohnt es sich, die wichtigsten Grundschritte noch einmal in unserem R-Tutorial nachzulesen. Dort finden Sie Hinweise zu …

R-Tutorial Teil 1

Abschnitt 2.1: Erstellen und Speichern von Skripten
Abschnitt 3.1: Laden von Bibliotheken
Abschnitt 3.2: Auswählen einzelner Spalten

R-Tutorial Teil 2

Abschnitt 2: Anlegen eines RStudio Projekts (Anstelle eines festen Working Directory empfiehlt es sich, ein RStudio Projekt anzulegen, da das oft praktischer ist)
Abschnitt 3: Datensätze einlesen

1.2 Vorbereitung in R

Bitte führen Sie nun folgende Schritte aus, um unser RStudio Projekt für die Analyse vorzubereiten:

Erstellen Sie ein neues RStudio Projekt (z.B. mit dem Namen Fragebogenentwicklung) und speichern Sie es an einem sinnvollen Ort ab.
Legen Sie ein neues R Skript an (z.B. mit dem Namen Modelltest), und speichern Sie es im Projektordner.

Laden Sie die für die Analyse benötigten Pakete:

library(psych) # für deskriptive Statistiken
library(ggplot2) # für Grafiken
library(lavaan) # für den Modelltest
library(semPlot) # zur graphischen Darstellung des Modells

Hiweis: Stellen Sie sicher, dass die Pakete vorher installiert wurden.

Laden Sie den Datensatz, den wir in diesem Tutorial verwenden werden, herunter und speichern Sie diesen in Ihrem Projektordner.
Lesen Sie den Datensatz in Ihrem Skript mit dem Befehl read.csv() ein (wir verwenden hier nicht read.csv2(), da der Datensatz im englischen .csv-Format vorliegt). Weisen Sie dem Datensatz das Objekt neo zu:
```
neo <- read.csv("NEO_original.csv")
```

1.3 Kurze Wiederholung: Befehle für Deskriptivstatistik

# Spalte "E1" auswählen
neo$E1

# Spalten "E1" und "E2" auswählen 
neo[, c("E1", "E2")]

# Deskriptive Statistiken für die Spalten "E1", "E2", "E3", "E4"
describe(neo[, c("E1", "E2", "E3", "E4")])

# Verteilung des Items "E1"
barplot(table(neo$E1)) # oder 
hist(neo$E1) # oder 
ggplot(neo, aes(x = E1)) + geom_bar()

# Streudiagramm 
plot(neo$E1, neo$E3) # oder 
ggplot(neo, aes(x = E1, y = E2)) + geom_jitter()

# Alle paarweisen Streudiagramme 
pairs.panels(neo[, c("E1", "E2", "E3", "E4")],
            density = FALSE,
            jiggle = TRUE,
            smooth = FALSE)

Output anzeigen

# Spalte "E1" auswählen
neo$E1

  [1] 3 0 4 2 3 0 2 3 3 2 2 3 1 1 2 4 1 1 1 1 4 3 3 2 3 2 2 3 1 1 2 4 3 2 1 3 3
 [38] 2 3 2 3 3 2 2 2 2 4 2 3 2 2 4 3 2 1 2 3 3 4 3 2 1 1 1 2 2 1 3 3 2 3 1 3 2
 [75] 3 3 2 4 0 4 1 2 3 3 2 3 3 2 2 3 2 1 2 3 3 2 3 2 1 1 2 1 1 3 3 2 1 1 2 2 2
[112] 1 3 2 3 4 1 4 3 3 1 4 3 2 2 1 1 4 3 1 0 4 1 2 2 3 2 1 3 2 4 1 2 2 3 1 1 3
[149] 1 2 3 3 2 2 0 2 1 2 2 0 1 3 1 2 1 3 3 1 4 4 2 1 2 2 3 1 3 2 2 2 3 2 1 2 3
[186] 2 3 2 1 3 3 3 3 2 2 2 3 2 2 3 2 3 3 3 2 3 1 3 3 3 1 4 4 3 1 3 4 2 3 3 2 3
[223] 1 1 2 0 1 3 1 3 3 2 2 2 2 4 3 3 0 2 3 3 3 3 2 2 3 2 2 4 3 3 1 4 2 3 3 2 1
[260] 1 1 2 3 3 4 2 3 2 2 4 2 4 2 2 3 3 3 4 1 2 1 0 2 3 2 1 1 3 3 4 2 3 3 1 3 2
[297] 3 2 2 3 2 3 3 3 2 3 2 1 2 3 4 2 1 3 1 0 3 0 3 1 2 1 2 1 2 3 2 3 3 3 2 3 1
[334] 3 3 1 2 1 4 1 3 1 1 2 3 2 2 1 3 2 2 3 4 2 2 2 2 0 0 2 2 3 2 2 0 3 1 1 1 3
[371] 1 0 3 2 1 1 2 1 2 1 1 2 3 3 2 4 2 1 3 2 2 1 2 3 3 2 2 2 3 1 2 2 2 3 3 2 2
[408] 1 2 3 3 1 1 3 3 3 2 4 0 2 2 4 4 3 1 1 1 1 3 2 1 4 3 1 2 1 3 2 3 1 2 1 1 2
[445] 3 3 3 3 3 3 3 2 2 4 3 3 3 2 1 3 4 3 2 1 3 1 2 3 2 1 2 2 2 2 3 3 3 2 3 1 3
[482] 1 3 1 1 2 2 3 4 1 3 3 2 1 3 2 4 2 0 2 3 1 1 3 2 2 3 2 3 3 2 3 2 2 1 1 2 1
[519] 2 1 2 2 3 2 2 4 3 3 2 2 1 1 2 2 1 2 1 1 4 3 3 4 2 1 0 2 2 3 3 2 2 3 3 1 2
[556] 2 3 2 3 4 4 4 3 1 3 3

# Spalten "E1" und "E2" auszuwählen 
neo[, c("E1", "E2")]

# Deskriptive Statistiken für die Spalten "E1", "E2", "E3", "E4"
describe(neo[, c("E1", "E2", "E3", "E4")])

   vars   n mean   sd median trimmed  mad min max range  skew kurtosis   se
E1    1 566 2.21 0.98      2    2.20 1.48   0   4     4 -0.12    -0.60 0.04
E2    2 566 2.72 0.85      3    2.78 0.00   0   4     4 -0.57     0.22 0.04
E3    3 566 2.47 1.09      3    2.50 1.48   0   4     4 -0.33    -0.81 0.05
E4    4 566 2.93 0.84      3    2.99 1.48   0   4     4 -0.69     0.52 0.04

# Verteilung des Items "E1"
barplot(table(neo$E1)) # oder

hist(neo$E1) # oder

ggplot(neo, aes(x = E1)) + geom_bar()

# Streudiagramm 
plot(neo$E1, neo$E3) # oder

ggplot(neo, aes(x = E1, y = E2)) + geom_jitter()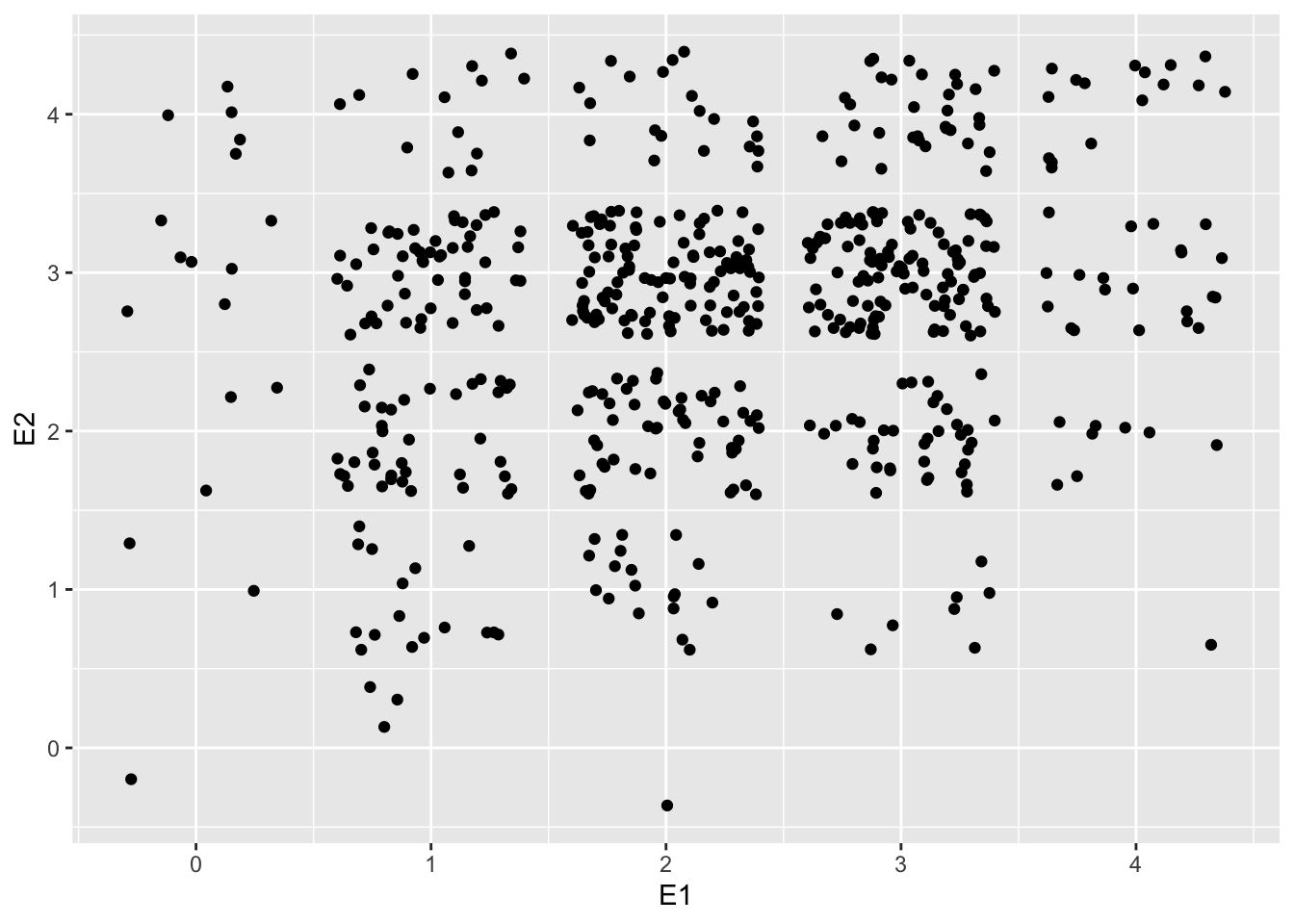

# Alle paarweisen Streudiagramme 
pairs.panels(neo[, c("E1", "E2", "E3", "E4")],
            density = FALSE,
            jiggle = TRUE,
            smooth = FALSE)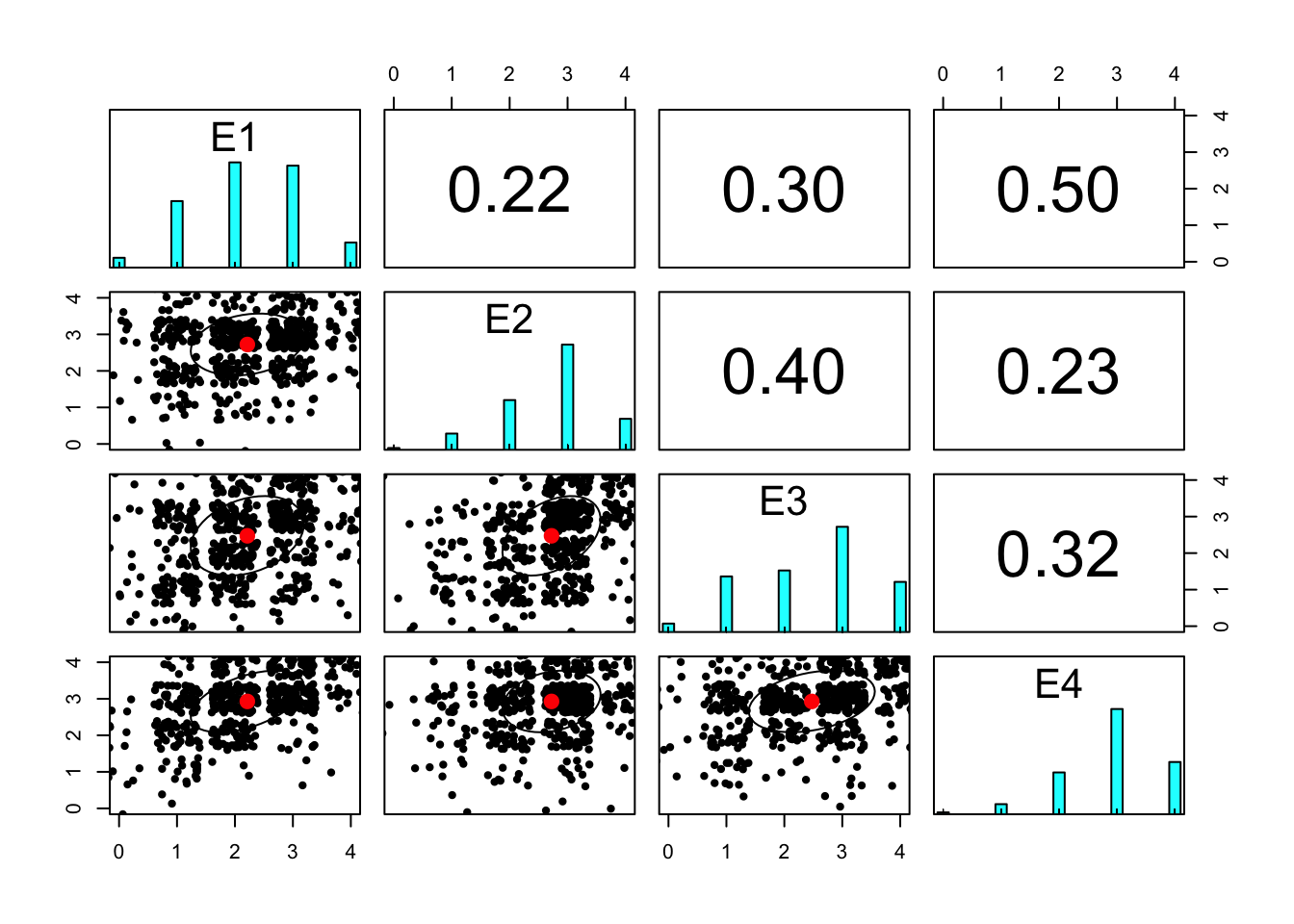

Mit diesen Schritten und Wiederholungen sind wir gut vorbereitet, um uns nun mit der Analyse von Testmodellen zu beschäftigen.

2 Konfirmatorische Faktorenanalyse (CFA)

2.1 Ziel der CFA

In diesem Abschnitt führen wir eine konfirmatorische Faktorenanalyse (CFA) mit dem {lavaan} Paket in R durch. Ziel ist es, das $\tau$-kongenerische Modell für den Faktor Extraversion anhand der Items E1, E2, …, E12 zu testen. Das $\tau$-kongenerische Modell nimmt an, dass alle Items eine latente Variable (hier: Extraversion) messen, aber unterschiedliche Gewichtungen bzw. Steigungen aufweisen können.

2.2 Schritte der CFA

1. Bestimmung der Anzahl an latenten Variablen

Da wir hier nur die Items E1, E2, …, E12 analysieren wollen, gehen wir für unser Modell davon aus, dass den Items nur eine einzige latente Variable Extraversion zugrunde liegt.

2. Spezifikation des Testmodells

Wir wollen hier ein eindimensionales $\tau$-kongenerische Modell betrachten. Zunächst spezifizieren wir das Modell im Textformat und weisen es dem Objekt model zu. Die Beschreibung des Modells folgt der speziellen Syntax des {lavaan} Pakets. Die latente Variable Extraversion nennen wir hier einfach e, und alle Items, die Extraversion messen, werden durch den Ausdruck e =~ E1 + E2 + ... + E12 mit dieser latenten Variable verbunden.

model <- "e =~ E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12"

3. Schätzung des Testmodells

Mit cfa() wird das Modell basierend auf den Daten in neo geschätzt. Die Ergebnisse und Parameterschätzungen werden im Objekt model_fit_extra gespeichert. Das Argument std.lv = TRUE sorgt dafür, dass die Varianz der latenten Variable auf 1 fixiert wird (siehe Normierung beim $\tau$-kongenerischen Modell in der Vorlesung). Mit meanstructure = TRUE wird festgelegt, dass Schwierigkeitsparameter für alle Items geschätzt werden sollen.

model_fit_extra <- cfa(model = model, data = neo,
  std.lv = TRUE, meanstructure = TRUE)

4. Evaluation der Modellpassung

Hinweis

Der folgende Output ist die Grundlage für die Beurteilung der Modellpassung sowie die Interpretation der Modellparameter.

Mit der Funktion summary() wird das Ergebnis des Modelltests und die Parameterschätzungen angezeigt. Mit dem Argument fit.measures = TRUE werden zusätzlich Fit-Indizes und Informationskriterien berechnet. Das Argument standardized = TRUE sorgt dafür, dass auch die Schätzwerte für die standardisierten Modellparameter angezeigt werden.

summary(model_fit_extra, standardized = TRUE, fit.measures = TRUE)

lavaan 0.6.17 ended normally after 16 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        36

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                               495.835
  Degrees of freedom                                54
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                              1827.444
  Degrees of freedom                                66
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.749
  Tucker-Lewis Index (TLI)                       0.693

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -8889.082
  Loglikelihood unrestricted model (H1)      -8641.165
                                                      
  Akaike (AIC)                               17850.164
  Bayesian (BIC)                             18006.353
  Sample-size adjusted Bayesian (SABIC)      17892.070

Root Mean Square Error of Approximation:

  RMSEA                                          0.120
  90 Percent confidence interval - lower         0.111
  90 Percent confidence interval - upper         0.130
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.083

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  e =~                                                                  
    E1                0.517    0.041   12.636    0.000    0.517    0.530
    E2                0.418    0.036   11.668    0.000    0.418    0.494
    E3                0.788    0.042   18.721    0.000    0.788    0.725
    E4                0.425    0.036   11.951    0.000    0.425    0.505
    E5                0.378    0.046    8.218    0.000    0.378    0.360
    E6                0.306    0.046    6.689    0.000    0.306    0.297
    E7                0.502    0.042   12.039    0.000    0.502    0.508
    E8                0.710    0.033   21.682    0.000    0.710    0.806
    E9                0.751    0.043   17.282    0.000    0.751    0.683
    E10               0.094    0.048    1.955    0.051    0.094    0.089
    E11               0.471    0.040   11.860    0.000    0.471    0.501
    E12               0.400    0.048    8.308    0.000    0.400    0.364

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .E1                2.214    0.041   53.964    0.000    2.214    2.268
   .E2                2.723    0.036   76.530    0.000    2.723    3.217
   .E3                2.473    0.046   54.123    0.000    2.473    2.275
   .E4                2.928    0.035   82.641    0.000    2.928    3.474
   .E5                1.809    0.044   40.947    0.000    1.809    1.721
   .E6                1.776    0.043   40.876    0.000    1.776    1.718
   .E7                1.760    0.042   42.342    0.000    1.760    1.780
   .E8                2.673    0.037   72.250    0.000    2.673    3.037
   .E9                2.337    0.046   50.566    0.000    2.337    2.125
   .E10               1.963    0.045   43.909    0.000    1.963    1.846
   .E11               2.389    0.039   60.555    0.000    2.389    2.545
   .E12               1.890    0.046   40.876    0.000    1.890    1.718

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .E1                0.685    0.044   15.717    0.000    0.685    0.720
   .E2                0.541    0.034   15.907    0.000    0.541    0.756
   .E3                0.560    0.041   13.621    0.000    0.560    0.474
   .E4                0.529    0.033   15.854    0.000    0.529    0.745
   .E5                0.962    0.059   16.402    0.000    0.962    0.870
   .E6                0.974    0.059   16.551    0.000    0.974    0.912
   .E7                0.725    0.046   15.837    0.000    0.725    0.742
   .E8                0.271    0.024   11.488    0.000    0.271    0.350
   .E9                0.646    0.045   14.317    0.000    0.646    0.534
   .E10               1.122    0.067   16.800    0.000    1.122    0.992
   .E11               0.659    0.042   15.871    0.000    0.659    0.749
   .E12               1.050    0.064   16.392    0.000    1.050    0.868
    e                 1.000                               1.000    1.000

Globaler Modellfit: Modelltest, Fit-Indices und Informationskriterien

Der Block $\texttt{Model Test User Model}$ im summary-Output liefert den Wert der Teststatistik, die Freiheitsgrade (df) und den p-Wert für den Modelltest. Die Nullhypothese testet, ob die Folgerungen aus dem $\tau$-kongenerischen Modell beibehalten werden können. Wenn die Alternativhypothese gilt, bedeutet dies, dass die Folgerungen verletzt sind und das $\tau$-kongenerische Modell würde unter der H1 abgelehnt werden. Unsere Daten liefern einen p-Wert von $p < 0.05$. Wir entscheiden uns also für die H1 und können nicht davon ausgehen, dass das eindimensionale $\tau$-kongenerische Modell in der Population gilt.

Die Fit-Indizes RMSEA, CFI und SRMR zeigen basierend auf den groben Richtwerten nach Hu & Bentler (1998) ein gemischtes Bild: Der RMSEA fällt zu hoch aus (Ziel: $RMSEA \leq 0.06$ bei $n > 250$). Der CFI ist zu niedrig (Ziel: $CFI \geq 0.95$). Nur der SRMR ist in Ordnung (Ziel: $SRMR \leq 0.1$).

Die Informationskriterien AIC und BIC werden zwar im Output berichtet, sind jedoch ohne ein Vergleichsmodell nicht hilfreich, da die absoluten Werte nicht wirklich interpretierbar sind.

Lokaler Modellfit: Inspektion der geschätzten Parameter und Modifikationsindizes

Der summary-Output enthält auch die Parameterschätzungen für das geprüfte Modell. In den Spalten $\texttt{z-value}$ und $\texttt{P(>|z|)}$ finden wir jeweils das Ergebnis der Signifikanztests, deren Nullhypothese jeweils besagt, dass der entsprechende Parameter in der Population den Wert 0 aufweist. Für die allermeisten im Modell geschätzten Parameter entscheidet sich der Test für die Alternativhypothese, dass sich der Wert in der Population von 0 unterscheidet. Für das Item E10 ist jedoch die Ladung nicht signifikant. Damit liegt hier eine mögliche Verletzung des lokalen Modellfits vor. Eventuell lädt das Item nicht auf die latente Variable Extraversion und trägt damit nichts zu deren Messung bei.

Da sowohl der globale als auch der lokale Modellfit Probleme aufzeigen, interessieren wir uns natürlich dafür, welche (Mis-)Spezifikationen des Modells dafür verantwortlich sein könnten. Dafür können wir uns mit der Funktion modindices() die Modifikationsindizes für das Modell ausgeben lassen. Das Argument sort. = TRUE sorgt dafür, dass die höchsten Modifikationsindizes ganz oben angezeigt werden.

modindices(model_fit_extra, sort. = TRUE, standardized = FALSE)

    lhs op rhs     mi    epc
41   E1 ~~  E4 65.824  0.220
43   E1 ~~  E6 51.479  0.257
81   E5 ~~ E10 50.790  0.315
42   E1 ~~  E5 40.072  0.227
64   E3 ~~  E8 37.789  0.160
83   E5 ~~ E12 33.339  0.251
89   E6 ~~ E12 30.790  0.241
93   E7 ~~ E11 28.373  0.165
47   E1 ~~ E10 28.137  0.202
95   E8 ~~  E9 25.663  0.133
98   E8 ~~ E12 24.070 -0.137
70   E4 ~~  E6 20.299  0.141
45   E1 ~~  E8 20.229 -0.107
79   E5 ~~  E8 19.694 -0.118
102 E10 ~~ E11 17.908  0.158
55   E2 ~~  E8 16.510  0.085
85   E6 ~~  E8 15.881 -0.106
40   E1 ~~  E3 15.380 -0.121
61   E3 ~~  E5 14.572 -0.134
76   E4 ~~ E12 14.306  0.124
73   E4 ~~  E9 14.104 -0.105
96   E8 ~~ E10 13.326 -0.102
66   E3 ~~ E10 12.907 -0.133
58   E2 ~~ E11 12.632 -0.095
49   E1 ~~ E12 10.820  0.123
69   E4 ~~  E5 10.678  0.102
72   E4 ~~  E8 10.355 -0.067
59   E2 ~~ E12  8.469 -0.096
78   E5 ~~  E7  7.628  0.101
82   E5 ~~ E11  7.062  0.093
46   E1 ~~  E9  6.959 -0.084
57   E2 ~~ E10  6.001 -0.083
67   E3 ~~ E11  5.581 -0.071
74   E4 ~~ E10  5.518  0.078
99   E9 ~~ E10  5.036 -0.087
48   E1 ~~ E11  4.693  0.066
50   E2 ~~  E3  4.423  0.057
52   E2 ~~  E5  4.176 -0.065
60   E3 ~~  E4  4.122 -0.054
90   E7 ~~  E8  4.010 -0.049
86   E6 ~~  E9  3.544 -0.069
80   E5 ~~  E9  3.210 -0.066
68   E3 ~~ E12  3.088 -0.064
39   E1 ~~  E2  2.607 -0.044
103 E10 ~~ E12  2.508  0.073
100  E9 ~~ E11  1.979 -0.044
77   E5 ~~  E6  1.759 -0.055
62   E3 ~~  E6  1.581 -0.044
71   E4 ~~  E7  1.484 -0.034
88   E6 ~~ E11  1.475 -0.043
104 E11 ~~ E12  1.060  0.038
44   E1 ~~  E7  1.032 -0.032
65   E3 ~~  E9  0.900  0.031
92   E7 ~~ E10  0.848  0.036
84   E6 ~~  E7  0.844 -0.034
75   E4 ~~ E11  0.649  0.021
97   E8 ~~ E11  0.627 -0.018
54   E2 ~~  E7  0.480 -0.019
51   E2 ~~  E4  0.463 -0.016
56   E2 ~~  E9  0.304 -0.016
91   E7 ~~  E9  0.270  0.017
63   E3 ~~  E7  0.136 -0.012
94   E7 ~~ E12  0.056 -0.009
87   E6 ~~ E10  0.040  0.009
53   E2 ~~  E6  0.012 -0.003
101  E9 ~~ E12  0.011  0.004

Die Modifikationsindizes zeigen kovariierende Fehlervariablen von Itempaaren an. Korrelierte Fehler könnten in einem neuen Testmodell spezifiziert werden. Jedoch sollten wenn möglich nur korrelierte Fehler aufgenommen werden, für die es eine überzeugende Erklärung aus der Theorie gibt. Viele korrelierte Fehler können auch darauf hindeuten, dass den Items eigentlich mehrere latente Variablen zugrunde liegen. Eventuell kann es informativ sein, die Struktur der Items (sowie die optimale Anzahl an latenten Variablen) mit einer Explorativen Faktorenanalyse zu untersuchen.

5. Interpretation der Modellparameter

Hinweis

Die Schätzungen der Modellparameter finden Sie in dem weiter oben präsentierten summary-Output.

Die Spalte $\texttt{Estimate}$ im Block $\texttt{Latent Variables}$ zeigt die Schätzwerte für die Steigungsparameter (Ladungen) der Items $\beta_i$. In der Spalte $\texttt{Std.all}$ finden wir die Schätzwertwerte für die standardisierten Steigungsparameter $\beta_{zi}$. Im eindimensionalen $\tau$-kongenerischen Modell entspricht die quadrierte standardisierte Ladung dem Anteil der Varianz des Items, der durch die latente Variable erklärt wird.

Beispiel: Das Item E1 hat einen geschätzten Steigungsparameter von $\hat{\beta}_{E1} = 0.517$ und einen geschätzten standardisierten Steigungsparameter von $\hat{\beta}_{zE1} = 0.530$.

Interpretation:

Steigt der Wert auf der latenten Variable Extraversion um eine Einheit, steigt die Itemantwort auf Item E1 im Mittel um $0.517$ Punkte.
Steigt der Wert auf der latenten Variable Extraversion um eine Standardabweichung, steigt die Itemantwort auf Item E1 im Mittel um $0.530$ Standardabweichungen.
Die latente Variable Extraversion erklärt $0.53^2 \cdot 100 = 28.09\%$ der Unterschiede in den Itemantworten von Item E1.

Unter $\texttt{Intercepts}$ finden wir die Schätzwerte für die Schwierigkeitsparameter der Items, die im $\tau$-kongenerischen Modell dem Erwartungswert jedes Items entsprechen.

Beispiel: Der geschätzte Schwierigkeitsparameter für Item E2 ist $\hat{\sigma}_{E2} = 2.723$.

Interpretation:

Die mittlere Itemantwort auf Item E2 für eine Person mit durchschnittlicher Extraversion beträgt $2.723$ Punkte.
Die mittlere Itemantwort auf Item E2 für eine zufällig gezogene Person beträgt $2.723$ Punkte.

Alternative Schätzung der Schwierigkeitsparameter

Wenn wir in der Console den Code mean(neo$E2) ausführen, bekommen wir ebenfalls das Ergebnis $2.723$, da wir mit dem Mittelwert den Erwartungswert $E(X_{E2})$ schätzen.

Die Spalte $\texttt{Estimate}$ im Block $\texttt{Variances}$ zeigt die Schätzwerte für die Fehlervarianzen der Items $VAR(\varepsilon_i)$. In der Spalte $\texttt{Std.all}$ finden wir die Schätzwertwerte für die standardisierte Fehlervarianz. Im eindimensionalen $\tau$-kongenerischen Modell entspricht die standardisierte Fehlervarianz dem Anteil der Varianz des Items, der nicht durch die latente Variable erklärt wird.

Beispiel: Die geschätzte Fehlervarianz für Item E3 beträgt $\widehat{VAR}(\varepsilon_{E3}) = 0.560$. Die geschätzte standardisierte Fehlervarianz für Item E3 beträgt $0.474$.

Interpretation:

Die latente Variable Extraversion erklärt $(1-0.474) \cdot 100 = 52.6\%$ der Unterschiede in den Itemantworten von Item E3.

Erwartungswert und Varianz der latenten Variable

Im $\tau$-kongenerischen Modell wird durch die Normierung der Erwartungswert der latenten Variable auf 0 fixiert und die Varianz der latenten Variable auf 1.

Die Fixierung der Varianz kann man in unserem Output im Bereich $\texttt{Variance}$ in der Zeile $\texttt{e}$ Spalte $\texttt{Estimate}$ erkennen. Da diese Varianz auf 1 fixiert und nicht geschätzt wurde, wird kein Standardfehler und auch kein Signifikanztest berechnet. In Testmodellen, bei denen die Varianz der latenten Variable frei geschätzt wird, findet sich in dieser Zeile stattdessen der entsprechende Schätzwert.

Wird in einem Testmodell der Erwartungswert der latenten Variable frei geschätzt und nicht fixiert, taucht im Bereich $\texttt{Intercepts}$ zusätzlich eine Zeile mit dem Namen der latenten Variable (hier $\texttt{e}$) auf, in der dann der entsprechende Schätzwert, Standardfehler und Signifikanztest angezeigt wird.

6. Grafische Darstellung des Modells

Mit semPaths() können wir das geschätzte Modell model_fit_extra grafisch darstellen. Die verschiedenen Argumente steuern die Formatierung der Abbildung und werden hier nicht im Detail erläutert. Für andere Datenbeispiele müssen Sie einfach das Modellobjekt austauschen und den Rest des Befehls eins zu eins übernehmen:

semPlot::semPaths(model_fit_extra, whatLabels = "std", intercepts = FALSE,
  style = "lisrel", layout = "tree2", rotation = 1)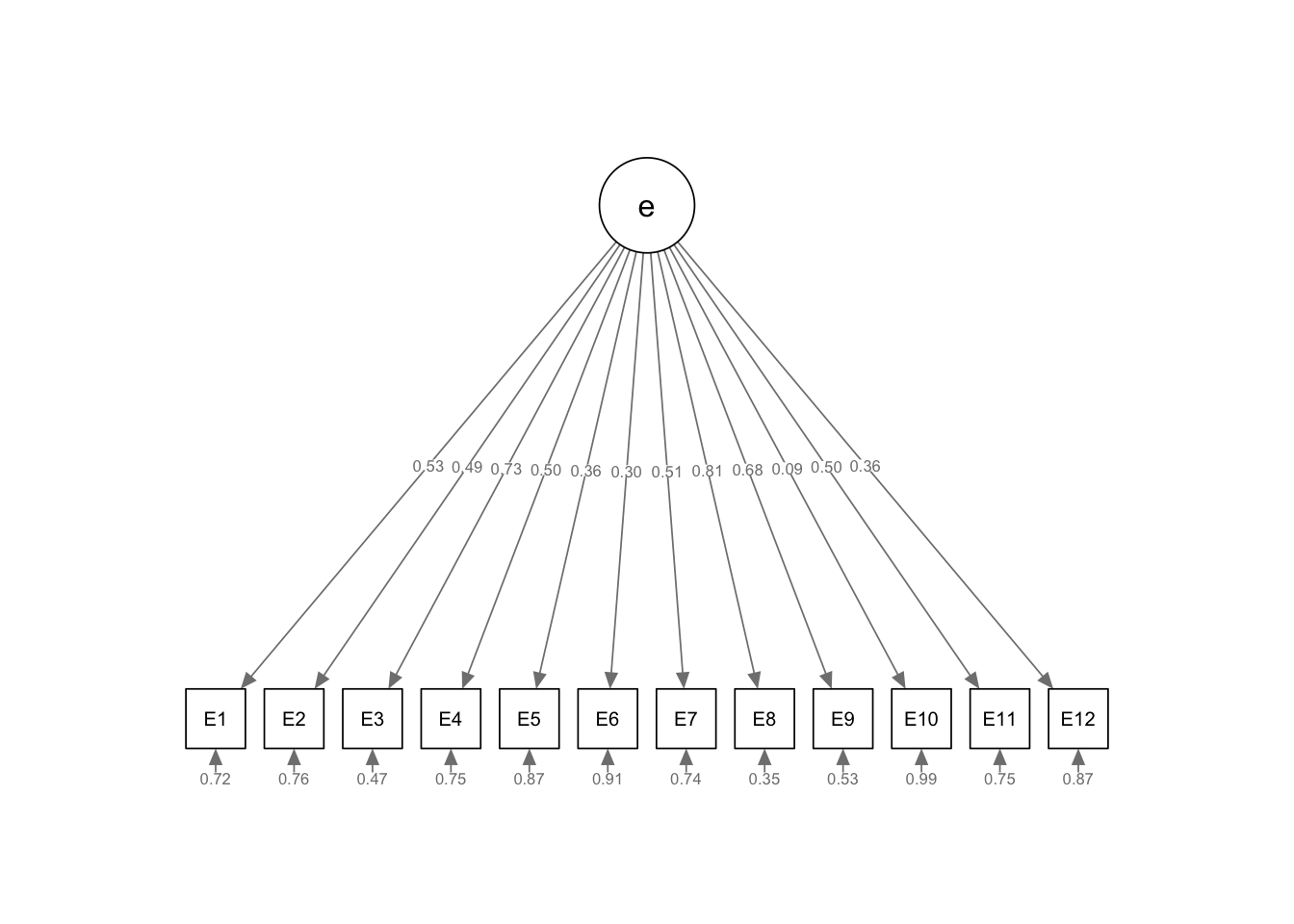

Die latente Variable $\texttt{e}$ (Extraversion) wird als Kreis dargestellt. Die manifesten Itemantworten $\texttt{E1,...,E12}$ werden als Rechtecke dargestellt. Die Zahlen neben den kurzen auf die Items weisenden Pfeile geben die Schätzwerte der standardisierten Fehlervarianzen an. Die Zahlen auf den langen Pfeilen zwischen der latenten Variable und den Items geben die Schätzwerte der standardisierten Steigungsparameter an.

3 Arbeitsauftrag

In dem folgenden Arbeitsauftrag können Sie die gleiche Analyse wie oben nochmals mit einem anderen Faktor als Extraversion ausführen. Die Analyse für Ihren Datensatz aus dem UK funktioniert später analog.

Arbeitsauftrag: Führen Sie eine CFA für die Skala Gewissenhaftigkeit (Variablennamen: C1, C2, … , C12) des Beispieldatensatzes NEO_original.csv:

Schätzen ein eindimensionales $\tau$-kongenerische Modell
Evaluieren Sie die Modellpassung (Modelltest, Fit-Indizes, Signifikanztests für die Parameter, Modifikationsindizes)
Interpretieren Sie die Schätzwerte der Modellparameter

Lösung

## CFA:
### Eindimensionales tau-kongenerisches Modell für Gewissenhaftigkeitsitems
model <- "c =~ C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12"

### Testmodell schätzen
model_fit_gewiss <- cfa(model = model, data = neo, std.lv = TRUE, meanstructure = TRUE)

### Modelltest, Fit-Indices, Informationskriterien, Parameterschätzungen anzeigen 
summary(model_fit_gewiss, standardized = TRUE, fit.measures = TRUE)

lavaan 0.6.17 ended normally after 20 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        36

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                               429.025
  Degrees of freedom                                54
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                              2174.573
  Degrees of freedom                                66
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.822
  Tucker-Lewis Index (TLI)                       0.783

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -8187.566
  Loglikelihood unrestricted model (H1)      -7973.054
                                                      
  Akaike (AIC)                               16447.132
  Bayesian (BIC)                             16603.322
  Sample-size adjusted Bayesian (SABIC)      16489.039

Root Mean Square Error of Approximation:

  RMSEA                                          0.111
  90 Percent confidence interval - lower         0.101
  90 Percent confidence interval - upper         0.121
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.065

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  c =~                                                                  
    C1                0.512    0.039   13.141    0.000    0.512    0.544
    C2                0.701    0.043   16.190    0.000    0.701    0.645
    C3                0.478    0.043   11.103    0.000    0.478    0.471
    C4                0.341    0.026   13.052    0.000    0.341    0.541
    C5                0.619    0.037   16.513    0.000    0.619    0.655
    C6                0.719    0.048   15.116    0.000    0.719    0.611
    C7                0.529    0.034   15.476    0.000    0.529    0.623
    C8                0.338    0.027   12.365    0.000    0.338    0.517
    C9                0.636    0.044   14.617    0.000    0.636    0.595
    C10               0.566    0.031   18.325    0.000    0.566    0.709
    C11               0.638    0.042   15.148    0.000    0.638    0.612
    C12               0.409    0.043    9.484    0.000    0.409    0.409

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .C1                2.650    0.040   67.033    0.000    2.650    2.818
   .C2                2.495    0.046   54.653    0.000    2.495    2.297
   .C3                2.611    0.043   61.135    0.000    2.611    2.570
   .C4                3.352    0.027  126.457    0.000    3.352    5.315
   .C5                2.459    0.040   61.970    0.000    2.459    2.605
   .C6                1.989    0.049   40.216    0.000    1.989    1.690
   .C7                2.726    0.036   76.338    0.000    2.726    3.209
   .C8                3.408    0.028  123.816    0.000    3.408    5.204
   .C9                2.555    0.045   56.813    0.000    2.555    2.388
   .C10               2.834    0.034   84.493    0.000    2.834    3.551
   .C11               2.797    0.044   63.800    0.000    2.797    2.682
   .C12               2.558    0.042   60.779    0.000    2.558    2.555

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .C1                0.623    0.040   15.735    0.000    0.623    0.704
   .C2                0.688    0.046   14.976    0.000    0.688    0.584
   .C3                0.804    0.050   16.089    0.000    0.804    0.778
   .C4                0.281    0.018   15.752    0.000    0.281    0.707
   .C5                0.509    0.034   14.874    0.000    0.509    0.571
   .C6                0.868    0.057   15.282    0.000    0.868    0.627
   .C7                0.442    0.029   15.185    0.000    0.442    0.612
   .C8                0.314    0.020   15.881    0.000    0.314    0.733
   .C9                0.740    0.048   15.408    0.000    0.740    0.646
   .C10               0.317    0.022   14.199    0.000    0.317    0.497
   .C11               0.680    0.045   15.273    0.000    0.680    0.625
   .C12               0.835    0.051   16.306    0.000    0.835    0.833
    c                 1.000                               1.000    1.000

## Modifikationsindices anzeigen
modindices(model_fit_gewiss, sort. = TRUE, standardized = FALSE)

    lhs op rhs     mi    epc
78   C5 ~~  C7 48.957  0.160
94   C7 ~~ C12 40.915  0.176
95   C8 ~~  C9 40.097  0.139
53   C2 ~~  C6 38.630  0.229
72   C4 ~~  C8 32.041  0.076
104 C11 ~~ C12 26.758 -0.176
54   C2 ~~  C7 24.575 -0.131
48   C1 ~~ C11 24.454  0.148
92   C7 ~~ C10 21.395  0.086
51   C2 ~~  C4 19.644 -0.091
76   C4 ~~ C12 19.119  0.094
44   C1 ~~  C7 19.101 -0.106
93   C7 ~~ C11 19.009 -0.113
79   C5 ~~  C8 17.226 -0.077
59   C2 ~~ C12 16.941 -0.142
58   C2 ~~ C11 15.636  0.129
74   C4 ~~ C10 14.713  0.055
70   C4 ~~  C6 11.778 -0.078
89   C6 ~~ C12 11.502 -0.130
67   C3 ~~ C11 10.807  0.110
66   C3 ~~ C10 10.036 -0.076
57   C2 ~~ C10  9.689 -0.073
39   C1 ~~  C2  9.353  0.093
85   C6 ~~  C8  8.034 -0.068
101  C9 ~~ C12  7.677 -0.098
61   C3 ~~  C5  6.966  0.078
75   C4 ~~ C11  6.330 -0.051
97   C8 ~~ C11  5.828 -0.051
80   C5 ~~  C9  5.783 -0.070
91   C7 ~~  C9  5.467 -0.063
83   C5 ~~ C12  4.900  0.066
81   C5 ~~ C10  4.568 -0.043
103 C10 ~~ C12  4.568  0.052
102 C10 ~~ C11  3.904 -0.045
96   C8 ~~ C10  3.293  0.027
63   C3 ~~  C7  3.215 -0.049
56   C2 ~~  C9  3.069  0.059
50   C2 ~~  C3  3.026  0.059
71   C4 ~~  C7  2.608  0.026
88   C6 ~~ C11  2.531  0.057
69   C4 ~~  C5  2.182 -0.026
55   C2 ~~  C8  2.093 -0.031
84   C6 ~~  C7  1.668 -0.038
42   C1 ~~  C5  1.634 -0.034
46   C1 ~~  C9  1.566 -0.039
77   C5 ~~  C6  1.508 -0.039
41   C1 ~~  C4  1.494 -0.023
65   C3 ~~  C9  1.395 -0.041
47   C1 ~~ C10  1.155 -0.023
60   C3 ~~  C4  1.075 -0.022
43   C1 ~~  C6  1.071  0.035
82   C5 ~~ C11  0.705  0.024
100  C9 ~~ C11  0.623  0.026
64   C3 ~~  C8  0.610 -0.017
86   C6 ~~  C9  0.525  0.027
40   C1 ~~  C3  0.434  0.021
52   C2 ~~  C5  0.333  0.017
73   C4 ~~  C9  0.330  0.012
62   C3 ~~  C6  0.295 -0.021
45   C1 ~~  C8  0.290 -0.011
68   C3 ~~ C12  0.290  0.019
90   C7 ~~  C8  0.254 -0.009
98   C8 ~~ C12  0.140 -0.008
87   C6 ~~ C10  0.121  0.009
99   C9 ~~ C10  0.070 -0.006
49   C1 ~~ C12  0.060  0.008

### Geschätztes Modell grafisch darstellen
semPlot::semPaths(model_fit_gewiss, whatLabels = "std", intercepts = FALSE, 
                  style = "lisrel", layout = "tree2", rotation = 1)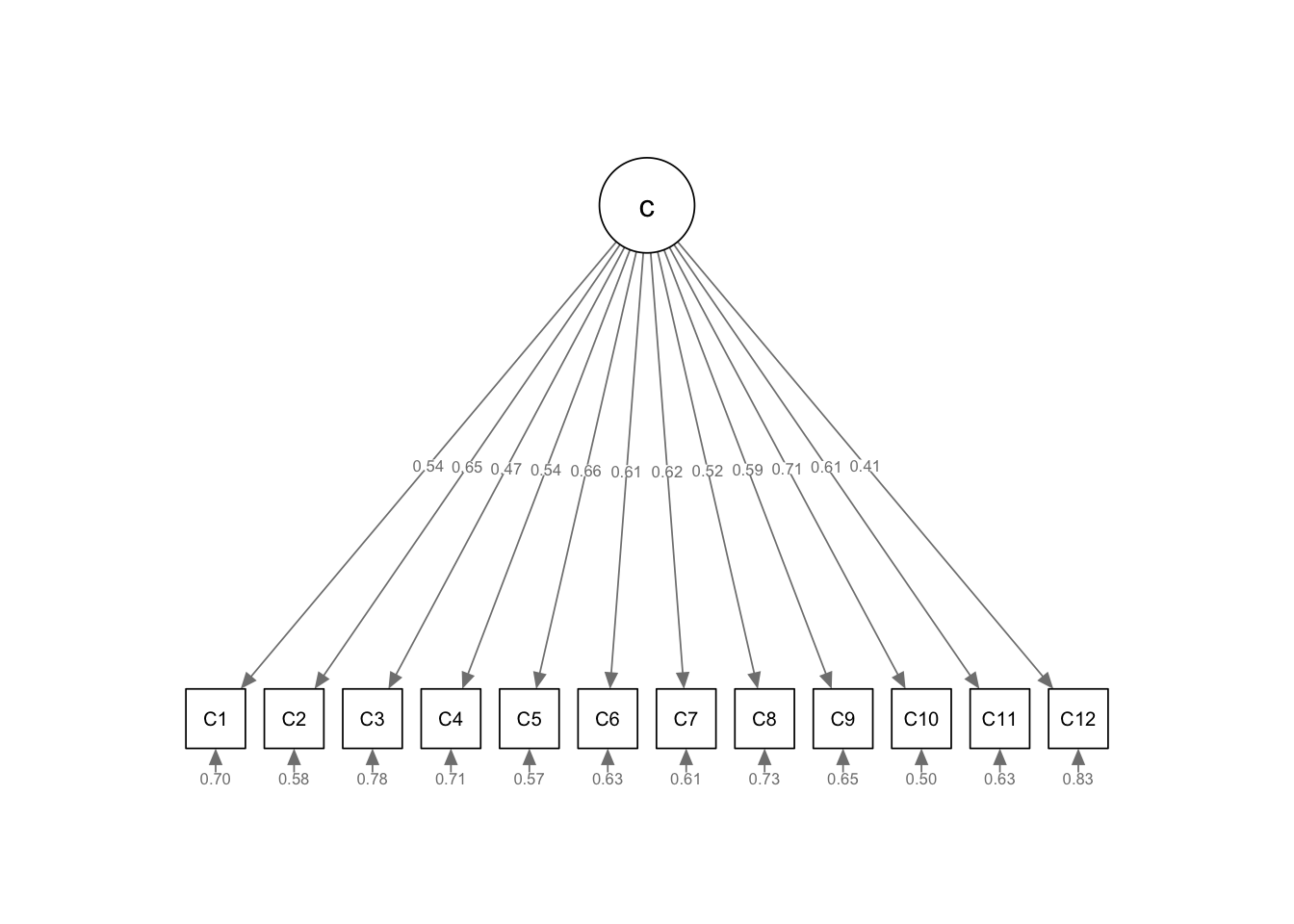

Kurze Zusammenfassung:

Der Modelltest entscheidet sich für die $H_1$ und lehnt damit das eindimensionale $tau$-kongenerische Testmodell für die Gewissenhaftigkeitsitems in der Population ab.
Auch die Fit-Indices RMSEA und CFI zeigen Probleme beim globalen Modellfit an, wohingegen der SRMR basierend auf den groben Richtwerten von Hu & Bentler (1998) ok ausfällt.
Hinsichtlich des lokalen Modellfits sind die Signifikanztests für die Modellparameter alle signifikant und damit unauffällig.
Jedoch zeigen die Modifikationsindices korrelierte Messfehler an.
Für die Interpretation der verschiedenen Modellparameter orientieren Sie sich bitte am Beispiel der Extraversionsskala.

4 Bonus: Strengere Testmodelle

Hinweis

In unserem Datenbeispiel haben wir nur das $\tau$-kongenerische Modell betrachtet. Auch bei diesem Testmodell mit den am wenigsten strengen Annahmen, scheint eine deutliche Verletzung des Modellfits vorzuliegen. Daher betrachten wir keine der noch strengeren Modelle. Die ein schlechter Modellfit für das $\tau$-kongenerische Modell der Normalfall ist, sind strengere Testmodelle in der Praxis nicht wirklich relevant.

Falls Sie die Analyse der strengeren Testmodelle trotzdem interessiert, können Sie sich diese im Folgenden ansehen.

4.1 $\tau$-kongenerisches Modell in einer anderen Schreibweise

Wir nutzen eine andere, ausführlichere Schreibweise für das $\tau$-kongenerische Modell:

Das Ergebnis ist dasselbe wie bei dem oberen Befehl

model <- "e =~ NA*E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12
1          E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12 ~ 1
2          e ~ 0
3          e ~~ 1*e"

1: In der 2. Zeile wird festgelegt, dass die Schwierigkeitsparameter frei geschätzt werden sollen:
E1 + ... + E12 ~ 1
2: $E(\theta)$ wird auf $0$ fixiert: e ~ 0
3: $Var(\theta)$ wird auf $1$ fixiert: e ~~ 1*e

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

Output anzeigen

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

lavaan 0.6.17 ended normally after 16 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        36

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                               495.835
  Degrees of freedom                                54
  P-value (Chi-square)                           0.000

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  e =~                                                
    E1                0.517    0.041   12.636    0.000
    E2                0.418    0.036   11.668    0.000
    E3                0.788    0.042   18.721    0.000
    E4                0.425    0.036   11.951    0.000
    E5                0.378    0.046    8.218    0.000
    E6                0.306    0.046    6.689    0.000
    E7                0.502    0.042   12.039    0.000
    E8                0.710    0.033   21.682    0.000
    E9                0.751    0.043   17.282    0.000
    E10               0.094    0.048    1.955    0.051
    E11               0.471    0.040   11.860    0.000
    E12               0.400    0.048    8.308    0.000

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1                2.214    0.041   53.964    0.000
   .E2                2.723    0.036   76.530    0.000
   .E3                2.473    0.046   54.123    0.000
   .E4                2.928    0.035   82.641    0.000
   .E5                1.809    0.044   40.947    0.000
   .E6                1.776    0.043   40.876    0.000
   .E7                1.760    0.042   42.342    0.000
   .E8                2.673    0.037   72.250    0.000
   .E9                2.337    0.046   50.566    0.000
   .E10               1.963    0.045   43.909    0.000
   .E11               2.389    0.039   60.555    0.000
   .E12               1.890    0.046   40.876    0.000
    e                 0.000                           

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    e                 1.000                           
   .E1                0.685    0.044   15.717    0.000
   .E2                0.541    0.034   15.907    0.000
   .E3                0.560    0.041   13.621    0.000
   .E4                0.529    0.033   15.854    0.000
   .E5                0.962    0.059   16.402    0.000
   .E6                0.974    0.059   16.551    0.000
   .E7                0.725    0.046   15.837    0.000
   .E8                0.271    0.024   11.488    0.000
   .E9                0.646    0.045   14.317    0.000
   .E10               1.122    0.067   16.800    0.000
   .E11               0.659    0.042   15.871    0.000
   .E12               1.050    0.064   16.392    0.000

Aufgrund der ausführlicheren Modell-Schreibweise müssen die Argumente std.lv = TRUE und meanstructure = TRUE diesmal nicht im Modelltest gesetzt werden.

4.2 essentiell $\tau$-äquivalentes Modell für Extraversion:

1model <- "e =~ 1*E1 + 1*E2 + 1*E3 + 1*E4 + 1*E5 + 1*E6 +
               1*E7 + 1*E8 + 1*E9 + 1*E10 + 1*E11 + 1*E12
          E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12 ~ 1 
2          e ~ 0
3          e ~~ e"

1: Steigungsparameter $\beta$ auf $1$ fixieren: ~ 1*E1 + ... 1*E12
2: $E(\theta)$ auf $0$ fixieren: e ~ 0
3: Die Varianz wird frei geschätzt (und nicht wie im $\tau$-kongenerischen Modell auf $1$ fixiert)

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

Output anzeigen

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

lavaan 0.6.17 ended normally after 20 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        25

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                               687.208
  Degrees of freedom                                65
  P-value (Chi-square)                           0.000

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  e =~                                                
    E1                1.000                           
    E2                1.000                           
    E3                1.000                           
    E4                1.000                           
    E5                1.000                           
    E6                1.000                           
    E7                1.000                           
    E8                1.000                           
    E9                1.000                           
    E10               1.000                           
    E11               1.000                           
    E12               1.000                           

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1                2.214    0.039   56.550    0.000
   .E2                2.723    0.038   70.841    0.000
   .E3                2.473    0.042   58.298    0.000
   .E4                2.928    0.036   81.235    0.000
   .E5                1.809    0.045   40.262    0.000
   .E6                1.776    0.046   38.571    0.000
   .E7                1.760    0.042   42.280    0.000
   .E8                2.673    0.035   77.148    0.000
   .E9                2.337    0.043   53.763    0.000
   .E10               1.963    0.050   39.079    0.000
   .E11               2.389    0.040   60.159    0.000
   .E12               1.890    0.047   40.288    0.000
    e                 0.000                           

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    e                 0.263    0.019   13.801    0.000
   .E1                0.605    0.039   15.513    0.000
   .E2                0.573    0.037   15.441    0.000
   .E3                0.756    0.048   15.776    0.000
   .E4                0.472    0.031   15.145    0.000
   .E5                0.880    0.055   15.924    0.000
   .E6                0.937    0.059   15.979    0.000
   .E7                0.718    0.046   15.720    0.000
   .E8                0.417    0.028   14.920    0.000
   .E9                0.807    0.051   15.843    0.000
   .E10               1.165    0.072   16.145    0.000
   .E11               0.630    0.040   15.565    0.000
   .E12               0.983    0.061   16.019    0.000

4.3 $\tau$-äquivalentes Modell für Extraversion:

model <- "e =~ 1*E1 + 1*E2 + 1*E3 + 1*E4 + 1*E5 + 1*E6 + 
               1*E7 + 1*E8 + 1*E9 + 1*E10 + 1*E11 + 1*E12
1          E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12 ~ 0
2          e ~ 1
          e ~~ e"

1: Dieses Modell hat keine Schwierigkeitsparameter, deshalb steht hier ~ 0
2: wir brauchen also auch keine Normierung für den Erwartungswert: e ~ 1

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

Output anzeigen

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

lavaan 0.6.17 ended normally after 32 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        14

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                              1980.764
  Degrees of freedom                                76
  P-value (Chi-square)                           0.000

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  e =~                                                
    E1                1.000                           
    E2                1.000                           
    E3                1.000                           
    E4                1.000                           
    E5                1.000                           
    E6                1.000                           
    E7                1.000                           
    E8                1.000                           
    E9                1.000                           
    E10               1.000                           
    E11               1.000                           
    E12               1.000                           

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1                0.000                           
   .E2                0.000                           
   .E3                0.000                           
   .E4                0.000                           
   .E5                0.000                           
   .E6                0.000                           
   .E7                0.000                           
   .E8                0.000                           
   .E9                0.000                           
   .E10               0.000                           
   .E11               0.000                           
   .E12               0.000                           
    e                 2.316    0.024   96.159    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    e                 0.258    0.020   13.188    0.000
   .E1                0.624    0.041   15.322    0.000
   .E2                0.755    0.048   15.585    0.000
   .E3                0.787    0.050   15.635    0.000
   .E4                0.888    0.056   15.771    0.000
   .E5                1.151    0.072   16.012    0.000
   .E6                1.247    0.078   16.074    0.000
   .E7                1.046    0.066   15.930    0.000
   .E8                0.559    0.037   15.148    0.000
   .E9                0.804    0.051   15.660    0.000
   .E10               1.282    0.080   16.095    0.000
   .E11               0.626    0.041   15.329    0.000
   .E12               1.177    0.073   16.030    0.000

4.4 essentiell paralleles Modell für Extraversion:

model <- "e =~ 1*E1 + 1*E2 + 1*E3 + 1*E4 + 1*E5 + 1*E6 + 
               1*E7 + 1*E8 + 1*E9 + 1*E10 + 1*E11 + 1*E12
1          E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12 ~ 1
2          E1 ~~ var*E1
          E2 ~~ var*E2
          E3 ~~ var*E3
          E4 ~~ var*E4
          E5 ~~ var*E5
          E6 ~~ var*E6
          E7 ~~ var*E7
          E8 ~~ var*E8
          E9 ~~ var*E9
          E10 ~~ var*E10
          E11 ~~ var*E11
          E12 ~~ var*E12
3          e ~ 0
4          e ~~ e"

1: Wir haben wieder Schwierigkeitsparameter, deshalb steht hier ~ 1
2: Die Varianzen sollen gleich sein: E1 ~~ var*E1 etc.
3: Normierung: e ~ 0
4: Varianz wird frei geschätzt: e ~~ e

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

Output anzeigen

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

lavaan 0.6.17 ended normally after 23 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        25
  Number of equality constraints                    11

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                               922.984
  Degrees of freedom                                76
  P-value (Chi-square)                           0.000

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  e =~                                                
    E1                1.000                           
    E2                1.000                           
    E3                1.000                           
    E4                1.000                           
    E5                1.000                           
    E6                1.000                           
    E7                1.000                           
    E8                1.000                           
    E9                1.000                           
    E10               1.000                           
    E11               1.000                           
    E12               1.000                           

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1                2.214    0.042   52.847    0.000
   .E2                2.723    0.042   64.994    0.000
   .E3                2.473    0.042   59.047    0.000
   .E4                2.928    0.042   69.886    0.000
   .E5                1.809    0.042   43.189    0.000
   .E6                1.776    0.042   42.387    0.000
   .E7                1.760    0.042   42.008    0.000
   .E8                2.673    0.042   63.813    0.000
   .E9                2.337    0.042   55.799    0.000
   .E10               1.963    0.042   46.858    0.000
   .E11               2.389    0.042   57.023    0.000
   .E12               1.890    0.042   45.129    0.000
    e                 0.000                           

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1       (var)    0.748    0.013   55.794    0.000
   .E2       (var)    0.748    0.013   55.794    0.000
   .E3       (var)    0.748    0.013   55.794    0.000
   .E4       (var)    0.748    0.013   55.794    0.000
   .E5       (var)    0.748    0.013   55.794    0.000
   .E6       (var)    0.748    0.013   55.794    0.000
   .E7       (var)    0.748    0.013   55.794    0.000
   .E8       (var)    0.748    0.013   55.794    0.000
   .E9       (var)    0.748    0.013   55.794    0.000
   .E10      (var)    0.748    0.013   55.794    0.000
   .E11      (var)    0.748    0.013   55.794    0.000
   .E12      (var)    0.748    0.013   55.794    0.000
    e                 0.245    0.018   13.390    0.000

4.5 paralleles Modell für Extraversion:

model <- "e =~ 1*E1 + 1*E2 + 1*E3 + 1*E4 + 1*E5 + 1*E6 + 
               1*E7 + 1*E8 + 1*E9 + 1*E10 + 1*E11 + 1*E12
1          E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12 ~ 0
          E1 ~~ var*E1
          E2 ~~ var*E2
          E3 ~~ var*E3
          E4 ~~ var*E4
          E5 ~~ var*E5
          E6 ~~ var*E6
          E7 ~~ var*E7
          E8 ~~ var*E8
          E9 ~~ var*E9
          E10 ~~ var*E10
          E11 ~~ var*E11
          E12 ~~ var*E12
2          e ~ 1
3          e ~~ e"

1: Da wir keine Schwierigkeitsparameter haben steht in der 2. Zeile: ~ 0
2: Der Erwartungswert der latenten Variable wird frei geschätzt: e ~ 1
3: Die Varianz der latenten Variable wird frei geschätzt: e ~~ e

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

Output anzeigen

model_fit_extra <- cfa(model = model, data = neo)
summary(model_fit_extra)

lavaan 0.6.17 ended normally after 23 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        14
  Number of equality constraints                    11

  Number of observations                           566

Model Test User Model:
                                                      
  Test statistic                              2161.582
  Degrees of freedom                                87
  P-value (Chi-square)                           0.000

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  e =~                                                
    E1                1.000                           
    E2                1.000                           
    E3                1.000                           
    E4                1.000                           
    E5                1.000                           
    E6                1.000                           
    E7                1.000                           
    E8                1.000                           
    E9                1.000                           
    E10               1.000                           
    E11               1.000                           
    E12               1.000                           

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1                0.000                           
   .E2                0.000                           
   .E3                0.000                           
   .E4                0.000                           
   .E5                0.000                           
   .E6                0.000                           
   .E7                0.000                           
   .E8                0.000                           
   .E9                0.000                           
   .E10               0.000                           
   .E11               0.000                           
   .E12               0.000                           
    e                 2.245    0.023   96.271    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
   .E1       (var)    0.912    0.016   55.794    0.000
   .E2       (var)    0.912    0.016   55.794    0.000
   .E3       (var)    0.912    0.016   55.794    0.000
   .E4       (var)    0.912    0.016   55.794    0.000
   .E5       (var)    0.912    0.016   55.794    0.000
   .E6       (var)    0.912    0.016   55.794    0.000
   .E7       (var)    0.912    0.016   55.794    0.000
   .E8       (var)    0.912    0.016   55.794    0.000
   .E9       (var)    0.912    0.016   55.794    0.000
   .E10      (var)    0.912    0.016   55.794    0.000
   .E11      (var)    0.912    0.016   55.794    0.000
   .E12      (var)    0.912    0.016   55.794    0.000
    e                 0.232    0.018   12.630    0.000

Arbeitsauftrag: Konfirmatorische Faktorenanalyse

1 Einführung

1.1 Auffrischung der R Grundlagen

1.2 Vorbereitung in R

1.3 Kurze Wiederholung: Befehle für Deskriptivstatistik

2 Konfirmatorische Faktorenanalyse (CFA)

2.1 Ziel der CFA

2.2 Schritte der CFA

1. Bestimmung der Anzahl an latenten Variablen

2. Spezifikation des Testmodells

3. Schätzung des Testmodells

4. Evaluation der Modellpassung

Globaler Modellfit: Modelltest, Fit-Indices und Informationskriterien

Lokaler Modellfit: Inspektion der geschätzten Parameter und Modifikationsindizes

5. Interpretation der Modellparameter

6. Grafische Darstellung des Modells

3 Arbeitsauftrag

4 Bonus: Strengere Testmodelle

4.1 \(\tau\)-kongenerisches Modell in einer anderen Schreibweise

4.2 essentiell \(\tau\)-äquivalentes Modell für Extraversion:

4.3 \(\tau\)-äquivalentes Modell für Extraversion:

4.4 essentiell paralleles Modell für Extraversion:

4.5 paralleles Modell für Extraversion: